13
Si nous examinons le loto connu de tout le monde et qui consiste, basiquement, à trouver 5 numéros parmi 49 numéros. Si l’ordre du tirage avait une importance, nous savons déjà qu’il s’agirait d’un arrangement de 5 numéros parmi 49 et nous savons comment le calculer : [latex]A_n^p = \frac {n!} {(n - p)!} = \frac {49!} {(49 - 5)!} = 228.826.080[/latex].
Mais dans le cas du loto, l’ordre du tirage n’a aucune importance. Il faut donc retirer, aux arrangements trouvés, l’ensemble des permutations de 5 numéros : [latex]\frac {\frac {49!} {(49 - 5)!}} {5!} = \frac {49!} {(49 - 5)! \times 5!} = 1.906.884[/latex] tirages de 5 numéros parmi 49 numéros sans aucune importance concernant l’ordre du tirage, ce qui s’appelle l’ensemble des combinaisons sans remise.
De façon plus mathématique, il s’agit de trouver combien de tirages de [latex]p-\acute el\acute ements[/latex] il est possible de faire parmi les éléments de l’ensemble [latex]X[/latex] sans que l’ordre n’ait d’importance, c’est à dire trouver le nombre de combinaisons de [latex]p-\acute el\acute ements[/latex] parmi [latex]n[/latex].
[latex]X = \left\{x_{1}, x_{2}, \ldots, x_{n}\right\}[/latex]
[latex]Card(X) = n[/latex]
[latex]p \le n[/latex]
[latex]Card(\left\{(a_{1}, a_{2}, \ldots, a_{p}) \mid a_{i} \in X, a_{i} ~distinct \right\})[/latex]
[latex]C_n^p = \begin{pmatrix} n \\ p \end{pmatrix} = \frac {A_n^p} {P_n} = \frac {\frac {n!} {(n - p)!}} {p!} = \frac {n!} {(n - p)! \times p!}[/latex]
La méthode de calcul des combinaisons sans remise peut parfaitement se substituer à celle utilisée pour calculer le nombre de permutations d’éléments d’un ensemble lorsque tous les éléments ne sont pas distincts. Revenons au cas du mot AUTORADIO. Le nombre de mots, avec ou sans signification, qu’il est possible d’écrire en permutant ces 9 lettres peut se voir de la façon suivante :
- Nous disposons de 9 positions pour placer les lettres
- Pour placer le A, il existe [latex]C_9^2 = \frac {9!} {(9 - 2)! \times 2!}[/latex] possibilités
- Pour placer le O, et partant du principe qu’il ne reste plus que 7 positions possibles, il existe [latex]C_7^2 = \frac {7!} {(7 - 2)! \times 2!}[/latex] possibilités
- Pour placer le U et partant du principe qu’il ne reste plus que 5 positions possibles, il existe alors 5 possibilités
- Pour placer le T et partant du principe qu’il ne reste plus que 4 positions possibles, il existe alors 4 possibilités
- Pour placer le R et partant du principe qu’il ne reste plus que 3 positions possibles, il existe alors 3 possibilités
- Pour placer le D et partant du principe qu’il ne reste plus que 2 positions possibles, il existe alors 2 possibilités
- Pour placer le I et partant du principe qu’il ne reste plus que 1 position possible, il existe alors 1 possibilité
Le nombre total d’anagrammes est donc :
[latex]\frac {9!} {(9 - 2)! \times 2!} \times \frac {7!} {(7 - 2)! \times 2!} \times 5 \times 4 \times 3 \times 2 \times 1[/latex]
[latex]= \frac {9!} {7! \times 2!} \times \frac {7!} {5! \times 2!} \times 5![/latex]
[latex]= \frac {9!} {2! \times 2!}[/latex]
Il nous reste à traiter un cas qui est de loin le plus lourd, car il sert à solutionner des situations qui peuvent devenir plus difficile à modéliser. Il s’agit de la combinaison avec remise, qui est bien la recherche de possibilités dans laquelle l’ordre n’a pas d’importance mais aussi dans laquelle chaque éléments peut apparaître plusieurs fois.
Utilisons un exemple simpliste, pouvant servir à mémoriser la formule, dans lequel nous avons [latex]n[/latex] cases et [latex]p[/latex] boules toutes identiques et devant être réparties dans ces [latex]n[/latex] cases. Si nous représentons la séparation entre les cases par une barre verticale et les boules par des ronds, une répartition de [latex]p[/latex] boules dans [latex]n[/latex] cases revient à placer sur un schéma [latex]n - 1[/latex] barres verticales (les deux cases extrêmes n’ayant besoin d’être délimitées que d’un seul côté) et [latex]p[/latex] ronds.
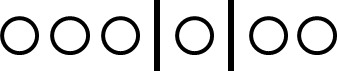
Dans cet exemple, [latex]n = 3[/latex] et [latex]p = 6[/latex], avec 3 boules dans la première case, une boule dans la deuxième et deux boules dans la troisième case. Le schéma est donc composé de [latex]p + n - 1[/latex] symboles parmi lesquels il faut choisir la place des [latex]p[/latex] ronds, les autres places étant automatiquement occupées par des barres verticales. Il s’agit donc de choisir [latex]p[/latex] places parmi [latex]p + n - 1[/latex], ce qui peut se faire de [latex]C_{p + n - 1}^{p}[/latex] façons différentes.
[latex]\Gamma_n^p = C_{n + p -1}^{p} = \begin{pmatrix} n + p - 1 \\ p \end{pmatrix} = \frac {(n + p - 1)!} {(n - 1)! \times p!}[/latex]
[latex]\Gamma_n^p[/latex]se lit « Gamma np » ou nombre de combinaisons, avec répétition ou remise, de [latex]p-\acute el\acute ements[/latex] parmi [latex]n[/latex].
