12

Si nous revenons à la questions initiale concernant les chevaux : « Sur une course de 18 chevaux, combien de tiercés sont possible, c’est à dire combien de podiums peut on anticiper ? », il y a plusieurs possibilités pour ces trois premières places, mais l’ordre d’arrivée est important et il n’y a pas de remise car tout cheval ayant une des trois premières places n’est plus pris en compte pour les autres places.

Nous avions vu que pour la première place, il existe 18 possibilités, mais pour la deuxième place il n’en existe plus que 17 puisque qu’un cheval ne peut être qu’à une seule place, et pour la troisième place il ne reste plus que 16 possibilités. Le nombre de podiums possibles est donc de : [latex]18 \times 17 \times 16[/latex]

Cette multiplication nous rappelle une factorielle à ceci près qu’il manque des termes. Pour le représenter sous forme de factorielle, nous pouvons utiliser l’astuce suivante : [latex]\frac {18 \times 17 \times 16 \times \ldots \times 2 \times 1} {15 \times 14 \times 13 \times \ldots \times 2 \times 1} = \frac {18!} {15!}[/latex]

Avec une formulation mathématique, ceci revient à chercher le nombre d’arrangements de [latex]p-listes[/latex] construites à partir de l’ensemble [latex]X[/latex] et dont les éléments des [latex]p-listes[/latex] sont tous distincts ou formulé différemment, le cardinal de l’ensemble des [latex]p-uplets[/latex]^[1], avec [latex]X[/latex] un ensemble constitué de [latex]n[/latex] éléments, sachant que tous les éléments des [latex]p-uplets[/latex] sont distincts et que [latex]p \le n[/latex].

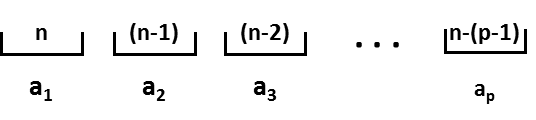
[latex]X = \left\{x_{1}, x_{2}, \ldots, x_{n}\right\}[/latex]

[latex]Card(X) = n[/latex]

[latex]p \le n[/latex]

[latex]Card(\left\{(a_{1}, a_{2}, \ldots, a_{p}) \mid a_{i} \in X, a_{i} ~distinct \right\})[/latex]

[latex]= n \times (n - 1) \times (n - 2) \times \ldots \times (n - (p - 1))[/latex]

[latex]= n \times (n - 1) \times (n - 2) \times \ldots \times (n - p + 1)[/latex]

[latex]= \frac {n \times (n - 1) \times (n - 2) \times \ldots \times (n - p + 1) \times (n - p) \times \ldots \times 2 \times 1} {(n - p) \times \ldots \times 2 \times 1}[/latex]

[latex]= \frac {n!} {(n - p)!} = A_n^p[/latex]

Le nombre d’arrangements de 3 chevaux parmi 18 est [latex]\frac {18!} {15!} = 4.896[/latex]

Il existe des cas d’arrangements pour lesquels il y a une possibilité de remise, c’est à dire qu’il est possible de remettre en jeu l’élément venant d’être choisi. Une illustration pourrait être un tirage au sort parmi 20 personnes, avec trois lots d’importance décroissante à gagner. La personne ayant été tirée pour gagner le premier lot est remise en jeu et peut donc gagner le deuxième lot et voire même le troisième lot lors du dernier tirage. On retombe ici sur un cas de dénombrement de base : [latex]Card(X^{p}) = n^{p} = Card(X)^{p}[/latex]

Il s’agit bien d’arrangement puisque l’ordre du tirage est important, le premier remportant le plus gros lot, le deuxième un lot moins important et le troisième le plus petit lot. Le nombre d’arrangements possible de trois personnes prises parmi 20, en partant du principe que toute personne tirée au sort peut continuer à participer au tirage est donc : [latex]20^{3} = 8.000[/latex]